Basics and Principle
Within the profile (grey), the air is resting, so ´normal´ atmospheric pressure exists. This pressure affects from inside at the upper and lower face, thus it´s force neutral (see arrows A). The air at the below face (red) is resting, however the wing is moving relative to the stationary air. This is equal to an air-flow (see arrow B) along the below face with the airplane´s speed. The air particles hit not perpendicular onto the face, but by a flat angle. That´s why the static pressure onto the below face is some reduced (see arrow C).
Along the upper face (green), a real air-flow exists, because the air particles fall into the relative void upside-rear. That suction is spreading also toward the front, especially along the upper surface. That´s why that ´artificial flow´ starts far in front and some below of the wing-nose. The suction affect spreads by sound speed, i.e. that wind relative to the wing exists only below sound speed. That real air motion of about 50 m/s adds to the airplane´s speed. So in comparison with the face below, the relative flow at the upper face is faster (see arrow D). That flow has stronger dynamic pressure and thus it can effect only reduced pressure onto the upper face (see arrow E).
The difference A-C presses down the below face. The difference A-E presses up the upper face. More simplistic: the total construction is pressed upward by the difference C-E. That resulting lift-force corresponds to the difference of dynamic pressures of these two air movements different fast.
Based on the different distances and the different quality of the surfaces, the flows along both faces show different speeds (see arrows B and D, upside slow, below faster). The flows show different dynamic pressures and correspondingly, they affect different static pressures onto the inner faces (see arrow C and E, stronger towards up, weaker towards down). Analogue to the forces at previous wing, here the lift-force comes up by the differences A-C and A-E respective direct by the difference C-E.
The lift force affects on the inner faces GF and HF, in total directed upward. The cylinder is fix mounted at the fuselage of the aircraft, so the lift force affects onto the whole body. All parts are stationary constructional elements, only the rotor is a turning part. The rotor blades are moving at horizontal level and they produce air movement only at the horizontal plane.
Force without Counter-Force
Previous model of the bowl-engine is transferred one-by-one from the motion processes and force effects at a wing. So this criticism same time concerns the common hypotheses of lift at wings quite generally. It´s common understanding, the different speeds are the trigger for lift force coming up. However, one does not agree in the assumption, why that difference is coming up. For example, it´s still told the naïve idea: the way upside is longer than the way below (no comment, the true cause is discussed comprehensive at previous mentioned chapter about ´Lift at Wings`).
Undisputed are the formula of dynamic and static pressure relations. Consequently applied, they deliver previous clear results. Nevertheless, they do not fit with the mechanical law, any action needs a corresponding counter action. Based on this common idea, air masses must be pushed down so strong, corresponding to the lift work for keeping an airplane at its momentary level - like e.g. it´s practice at helicopters.
Air-down / Aircraft-up
Based on the law of impulse-constant - the aircraft is affected by a lifting-impulse corresponding to the downward-impulse of air - a mass of 415 t must be accelerated down by 12 m/s. The acceleration of that air-mass-flow demands about 39.400 PS - correct determined by physical rules and common accepted result.
Really Impossible
Indeed, that´s a real impossibility. Previous calculations are correct. However it´s assumed, the air would show the properties of a solid body: an impulse on a (part-) face immediately would affect the whole mass. Opposite, one can not ´catch´ the air, the pressure is not forwarded mechanically, the air is compressible and escapes immediately into areas of less density, by sound speed, without feeding back (mechanical) counter-pressure. The wing simply can not reach enough air-masses in order to produce downward-current of that size, demanded by the view of impulse-constant respective the law of force / counter-force.
This mechanistical view is most common and it´s also suggested, the air upside of the wing would be drawn down, and behind the wing even deeper - so the aircraft correspondingly would rise up. Picture 05.17.02 once more shows previous profile A: the air is lifted at the front side, before falling down at the rear end (see arrows). Might be the air later will go on falling down, however with no importance for the lift (because up there are no mechanic lever-arms for balancing forces).
Dam-Up-Air / Push-Up-Aircraft
That ´pushing-up´ above the tilted plane of an air-cushion demands much thrust (and that´s why the rear-flaps are retracted short time after lift-off). That work of lifting by pushing-up of the airplane masses occurs corresponding to the mechanical laws. One must differ strongly the ´natural lift´ of wings - because that occurs by the totally different rules of hydro-static buoyancy.
Buyancy at Water and Air
Decisive for that buoyancy, all times is the difference of water-pressures onto the faces below and upside. With every meter of depth, the water-pressure increases by on ton, i.e. by 10000 N/m^2. For example, this becomes obvious if a wooden stick (F) is holt vertical within the water. If it´s released, the pressure vehemently catapults the stick out of the water.
We are steady exposed to the atmospheric pressure. However we merely register it´s weighting with about 100000 N/m^2, so corresponding to a water-pile of ten meter. The airs seams light, however the buoyancy is working like at the water. A balloon (G) filled up with air is nearby as heavy like the displaced air and is gliding around anyhow. A balloon (H) filled up with a light gas will rise up.
Accelerated molecular Speed
The normal atmospheric pressure weights outside at the balloon-shell, as the particles hit onto the material with their normal molecular speed. The particles inside hit some stronger versus the material as they are moving faster. Resulting is a difference of static pressures.
The air pressure is calculated by formula P=0.5*rho*v^2*0.7 = 109375 N/m^2 (density rho=1.25 kg/m^3m, molecular speed 500 m/s, factor 0.7 because the particles in average hit onto a face by an angle of 45 degree). If the added heat increases the molecular speed only by 3 m/s, a difference of more than 100 N/m^2 comes up. A balloon with 8 m radius has an effecting face of 200 m^2. The small difference of static pressures can keep gliding a cross-weight of 2000 kg. Further heat will rise up the balloon. The balloon will go on rising without further input of energy. Occasional heating must only balance the heat-losses.
Hydrostatic and Aerostatic Buoyancy
Here, the buoyancy force is caused exclusive by the difference of static pressures at the effective faces, e.g. based on different water-pressure at different depth. This difference can be increased ´artificial´, e.g. at that hot-air balloon with accelerating the molecular speed. Decisive all times are the pressure-relations direct at the border faces, here inside and outside the balloon-shell, quite near to the material.
A difference naturally come up also with air-flows, e.g. if a storm razes over the flat roof of a building. The wind has strong dynamic pressure and can affects pressure onto the roof corresponding weaker. The normal (now however relative stronger) atmospheric pressure within the building catapults the roof off.
At the other hand, that wind can be created ´artificially´, e.g. via suction effect above the face of a wing. The inevitable resulting difference of static pressures, direct at the border-layers above and below the wing, generates the lift-force.
Energy input is only necessary for the forward motion of the airplane, thus only for balancing the air-resistance. The ´buoyancy-force´ is resulting exclusive from the difference of static pressures, by the laws of hydro-statics respective rules of fluid-dynamics (and certainly not by the laws of solid-body-mechanics). Just corresponding with the processes at any wing, the effects are rebuild within the closed systems of bowl-engines.
Data of the A320
It´s realistically assumed, the flow along the upper face is faster by 50 m/s than along the face below. The dynamic flow-pressures are calculated for the upper and lower faces (PDO and PDU, O=oben=up, U=unten=below). The PD-difference is multiplied by the wing-face of 122 m^2, resulting the lift-force (P-Lift).
For the following climbing up, the mass is rising up alone by the surplus of buoyancy forces (e.g. at 560 km/h with 883 kN). Also at travel-speed within ´thin´ air, the lifting-force of 790 kN is stronger than demanded (the profile-example at chapter ´Lift at wing´ had an additional flow of 45 m/s, which here would result even better matching data).
The mass m = 70000 kg is accelerated with a = 1.5 m/s^2 at a runway of s = 2000 and after the time t = 52 s the speed v = 78 m/s is achieved, demanding a thrust Fb = 106 kN. Same time, the air-resistance must be overcome. With extended rear-flaps, the cross-section face might be A = 40 m^2 with Cw = 0.3, demanding up to 44 kN thrust. So at the end of the runway, 150 kN thrust force is necessary, available by the installed power of roundabout 210 kN.
If the rear flaps are retracted, the face will be reduced to A = 25 m^2 and also the Cw = 0.2. Decreasing density but increased speeds results stronger air-resistance, demanding stronger thrust (e.g. of 49 kN and 68 kN). The performance of the installed engines decreases linear with the density (e.g. at 140 kN and 87 kN). Finally these facts determine the optimum flight-level and travel-speed.
Force and Counter-Force
A wing does not float within air-less space. The wing is ´clamped´ by the atmospheric pressure, from upside and below with 10 t/m^2 respectively 10000 kg/m^2 respectively 100000 N/m^2. Caused by the relative flow direct at the border faces, a difference comes up at a size of about 6000 N/m^2 (row PD-Difference). So the pressure differs only by 6/100 between the upper and lower face - resulting lift-forces sufficient for lifting heavy aircrafts.
That´s the decisive difference: the air-resistance is compensated by the jet-engines via reaction (see row Fw with 44 kN, 49 kN und 68 kN). At great height and low density, the performance of the engines is very reduced. They are just able to compensate the strong air resistance (increased by fast travel-speed). Opposite and quite different, the buoyancy is generated by (hydro-) static rules (see row P-lift with 754 kN, 883 kN und 790 kN).
It´s clear stated: the thrust is only demanded for acceleration of the aircraft and its forward motion. That´s only the trigger for generating the buoyancy. It´s clear stated: the generated lift-force (row P-Lift) is stronger than the invested thrust-force (row Fw) by factor 11 and up to 18.
Some people mix-up these facts with a ´Perpetuum Mobile´. Realiter however, it´s only the clever usage of given forces of an open system. All pressure-forces used here, finally are based on the omnipresent gravity.
The fuselage has a diameter of four meter. At the rear area of the fuselage are installed the engines with total length about four meter. Each four units are installed at two levels. Each unit has fife round hollow cylinders at one shaft with one drive-motor. The boxes here are shaped like cones. The rotor can draw the air around convex glide-faces without resistance and same time, the air affects stronger pressure onto the concave stick-faces.
The radius of the rotor-blades is 0.65 m, covering a face of 1.33 m^2. Weighted averages are given at a radius of 0.45 m, respective at the circumference of 2.83 m. The performance can be controlled by the density, e.g. the system is driven with rho = 3 kg/m^3. The performance naturally is also controlled by the revolutions, here e.g. with 2400 RPM. The difference of the flow speeds along the glide- and stick-faces (GF and HF) is only to measure empirical. At wings the differences are 60 % to 25 %, here only 10 % are assumed.
The weighted speeds are 113 m/s and 102 m/s, the difference of dynamic flow pressures is 3642 N/m^2. Same time that´s the difference of static pressures (here about half of the lift-pressures at a wing). Multiplied by the effective faces, one unit will deliver a thrust force of about 24 kN and in total the eight engines about 193 kN (i.e. a size comparable to the present installed jet-engines).
Advantages of Aerostatic Thrust
At this bowl-engine, the thrust is done by the hydro- respective aero-static principle, which is much more effective. For example, all cylinders of previous engine in total contain only 10 kg of air, which is once accelerated up to about 100 m/s. Afterward the rotors must only keep the air rotating, all times running around along cone-shaped faces. Much less fuel is necessary (probably less than one tenth). The start weight is reduced, so the acceleration demands less thrust.
The internal installed bowl-engines replace the external jet-engines, so the air-resistance will be reduced (see picture 05.17.06). The performance of the bowl-engines is constant at all heights. The new engine is much lighter and easier to build with corresponding advantages of costs and for maintenance. Last but not least, these airplanes are silent like gliders.
These advantages are valid also for the new conception of helicopters, as described at previous chapter. There, not only the thrust is done with bowl-engines, but also the lift and the control functions. All units are integrated within the fuselage. This new helicopter causes no external air movements, flying and hovering quite silent (details see that chapter).
That´s no science-fiction. That´s only the clever usage of side-effects of the known behaviour of molecular movements of air-particles. The air-pressure-bowl-engine is tremendous effective because working by the rules of hydro- and aero-static buoyancy. Its background is the enormous energy of the atmospheric pressure, which by itself is an appearance of the omnipresent gravity. No patent application is done for this invention. Everybody may use these open-source ideas as he likes it.
Evert / 31.01.2016
At the previous chapter ´Air-Pressure Bowl-Engine´, the motion processes and force-effects at wings were transferred into a closed system. Basis of that principle is the well known effect of lift, like used by any airplane. However, the real cause of that appearance is contested by about ten different hypotheses. My considerations and comprehensive theory were published at chapter ´05.01. Lift at Wings´. Upside at picture 05.17.01, the air movements and affecting forces are sketched once more.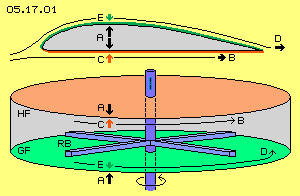 Reconstruct at closed System
Reconstruct at closed System
These processes are rebuild within the closed system of the air-pressure bowl-engine. Its general shape is a round hollow cylinder, like sketched at picture 05.17.01 below. The normal atmospheric pressure weights at all outside faces, force neutral in total (see arrows A). A rotor (blue) produces and maintains the ´artificial wind´. Its rotor-´blades´ (RB) are a right-angle profile, working not like normal props. They only keep the air steady rotating. The rotor-blades are moving above the below inner face by a short distance. This surface is most smooth, here called ´glide-face´ (GF, green). The distance to the inner face above is some larger. This surface is most rough, here called ´stick-face´ (HF, red).
Normally, nobody might understand why that stuff could work anyhow. The scientist knows exactly: these ideas contradict the law of actio=reactio, because no force can exist without counter-force. Since long, that´s a fundamental knowledge, deduced already from simple mechanical processes. That´s completely right - however fluids are no solid bodies and within fluids are valid quite other rules.
Just this is the assumption of the prevailing hypothesis. At chapter ´05.12. A380 and Lift´ were presented the calculations of a scientist (of a prestigious air- and spacecraft-faculty at a German university). The data for the A380 resulted in brief (for details see that chapter):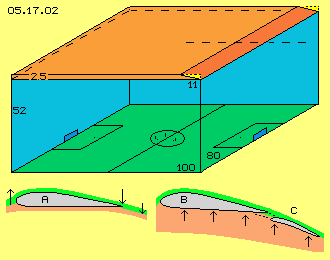 I wonder why these (mathematical consistent) results are not checked versus obvious reality. Based on the assumed density rho = 1 kg/m^3 that air-mass is equal to a volume of 415.000 m^3, sketched upside at picture 05.17.02. The A380 spans 80 m and it takes one second for crossing a football pitch (green) with the assumed speed of 100 m/s. An 18-floor-building (blue walls) of 52 m height would have likely volume. Upside right is marked the wing (dark-red) with its face of 850 m^2, 80 m wide and 11 m long, with an extreme angle of attack (yellow).
I wonder why these (mathematical consistent) results are not checked versus obvious reality. Based on the assumed density rho = 1 kg/m^3 that air-mass is equal to a volume of 415.000 m^3, sketched upside at picture 05.17.02. The A380 spans 80 m and it takes one second for crossing a football pitch (green) with the assumed speed of 100 m/s. An 18-floor-building (blue walls) of 52 m height would have likely volume. Upside right is marked the wing (dark-red) with its face of 850 m^2, 80 m wide and 11 m long, with an extreme angle of attack (yellow).
The wing can grasp a layer of air (light red) of 2,5 m height at its maximum, during that one second only 2.5*80*100=20000 m^3, not even 5 % of the involved volume. There is no chance for pushing down the remaining 95 % volume respective masses by 12 m/s.
Below right side, this picture shows a situation, where air indeed is pressed down: if the wing (B) is tilted and rear-flaps (C) are extended. Again however the downward-motion of air is without importance, but the air is dammed up, compressed, building an ´air-cushion´. The counter-pressure is pushing upward the faces (see arrows). However this works only near the ground. The downward pressure wave spreads with sound speed. The counter-pressure comes back only by half speed. It takes one tenth of a second for moving the wing-length of 11 m. The counter-pressure is running only some 15 m, so will miss the wing already by slow speed and short distances.
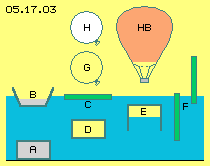 That well known process is sketched at picture 05.17.03. Within the water (blue) all bodies (A) with heavier specific weight sink down to the ground. A body (B and C) is swimming at the surface, if its mass is some less than the water displaced. If both are equal, the body (D) will glide anywhere within the water. If a box (E) is open below, the enclosed air is compressed until the pressure is balanced at the below border-face. If the inside pressure is stronger than the water-pressure at the upper face of the box, that body will rise up.
That well known process is sketched at picture 05.17.03. Within the water (blue) all bodies (A) with heavier specific weight sink down to the ground. A body (B and C) is swimming at the surface, if its mass is some less than the water displaced. If both are equal, the body (D) will glide anywhere within the water. If a box (E) is open below, the enclosed air is compressed until the pressure is balanced at the below border-face. If the inside pressure is stronger than the water-pressure at the upper face of the box, that body will rise up.
An interesting case is a hot-air balloon (HB): below it´s open so the air pressure inside and outside is balanced. Different however is the molecular speed of the air particles, which inside is accelerated by the heating. Some ´fast´ particles indeed are rising up within the balloon. Above this, anywhere the direction and speed of particles is exchanged at each collision, so the fast speed is forwarded from one particle to the next. The hot gas demands wider space, it´s lighter and thus rising up.
That´s the grave distinction to previous mechanic lifting: that pushing-up of the airplane-mass above the tilted plane of the air-cushion demands steady input of energy. Opposite here, only once must occur the heat-input and afterward, only the heat-losses must be compensated (comparable with friction-losses).
Previous statements are supported by A320-data shown at table 05.17.04. Three columns show the phases of starting, rising-up and travel-flight, at heights of 0 m, 4000 m and 8000 m, where the density is 1.2 kg/m^3, 0.8 kg/m^3 and 0.5 kg/m^3. The speeds are 280 km/h, 560 km/h and 840 km/h, respectively 78 m/s, 156 m/s and 234 m/s.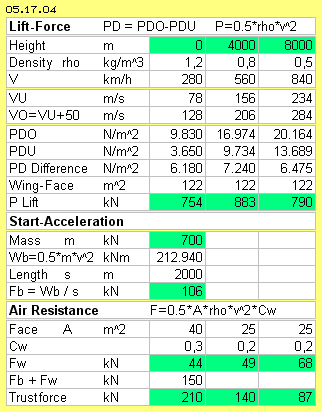 Already at the start-speed of 280 km/h sufficient lift-force (resp. buoyancy) exists for rising-up the A320 with its start-masse of 70 t (700 kN).
Already at the start-speed of 280 km/h sufficient lift-force (resp. buoyancy) exists for rising-up the A320 with its start-masse of 70 t (700 kN).
These data confirm, energy-input is used for the acceleration at the start and up to the travel speed. Additional energy-input is necessary for balancing the air resistance, however not for the lifting of the aircraft. Previous critical question about action / reaction now has an answer most clear: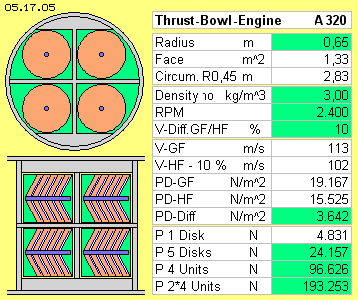 Horizontal like Vertical
Horizontal like Vertical
This process and the effects of pressure differences can also be realized within a closed system. The wings produce forces in vertical direction. Likely forces can be directed horizontal within a closed box. A bowl-engine thus can serve for the drive of an aircraft, e.g. like sketched at picture 05.17.05 and shown by data for an A320 airplane.
 When the thrust is done by reaction-principle, many tons of hot gases must be accelerated up to 300 m/s, on and on, demanding steady energy input. The weight of necessary fuel is one quart (at least) of the cross-weight at the start phase.
When the thrust is done by reaction-principle, many tons of hot gases must be accelerated up to 300 m/s, on and on, demanding steady energy input. The weight of necessary fuel is one quart (at least) of the cross-weight at the start phase.
ap0517e.pdf
is the print version of this chapter,
ap0517ae.pdf is a brief print version.
Pros and Cons for Bowl-Engines
Aero - Technology