Clear Principle
All around the cylinder exists normal atmospheric pressure AP = 100000 N/m^2, based on the density Rho = 1.2 kg/m^3 (the exact calculation of the atmospheric pressure is shown at chapter ´05.13. Explosion / Implosion´ at picture 05.13.01). Inside of the cylinder exists a density of Rho = 1.6 kg/m^3 and thus a static pressure IP = 130600 N/m^2.
The dynamic flow-pressure is calculated by known formula DP = 0.5*rho*v^2. So along the glide-face exists DPG = 0.5*1.6*100^2 = 8000 N/m^2. Along the stick-face exists DPH = 0.5*1.6*90^2 = 6500 N/m^2. The difference is DPD = 8000 - 6500 = 1.500 N/m^2.
The static pressure (of resting air) at the side faces is reduced by the dynamic flow pressure. So inside of the glide-face exists only the static pressure SPG = 130600 - 8000 = 122600 N/m^2. At the stick-face exists some higher static pressure SPH = 130600 - 6500 = 124100 N/m^2. At both side faces (of each 1 m^2) is weighting the normal atmospheric pressure AP = 100000 N/m^2 from outside, symmetrical and thus force-neutral. Based on the pressure difference at the inner side faces, however exists a thrust force of P = 1500 N, shifting the whole cylinder towards left.
These calculations are based on known formula at facts and thus they are undisputed. It´s also quite clear, the rotor needs few energy-input for keeping the air turning same direction all times. The usable thrust however is much stronger than the demanded energy-input. Nevertheless remain reservations, e.g. by the ´reverse-arguments: it can not be what may not be´. A concrete objection e.g. could be: the internal differing static pressures are suspended by material-tension within the cylinder-mantle, so no external affect can come up.
Thrust by Reaction
A tank filled up with water is installed at wheels, so it can roll along the ground. The water can flow off an opening towards right side. The water pressure is weighting (asymmetrical, without counter-pressure) at that part of the wall marked red. A thrust-force comes up (see red arrow), pushing that wall toards left (at first, the masses of water and the vehicle must be accelerated). Right side at this picture, two additional elements are drawn. They won´t increase the efficiency, but make that model comparable with the characteristics of the bowl-engine.
Analogue to the bowl-engine, different forces are affecting at opposite faces (here marked red and green). Both components will affect tension at the material of the vehicle (like mentioned upside). Nevertheless that pressure difference results the external effect of thrust.
At the centre of that vehicle is drawn a vertical pipe, where a pump P is lifting up the water back into the upper tank. Also that measurement is not really effective. This will only show, that reaction-principle in general is also working within a completely closed system. Included is also the ´motor´ for a continuous mode of the system (here that pump, at the bowl-engine the rotor). At both cases, the surrounding medium is not involved and not relevant (the ambient atmospheric pressure is force-neutral). The internal pressure-difference still produces the external effect of thrust for the complete unit.
At this example, likely (water-) pressure exists at faces of different size. Opposite, the faces of the bowl-engine are same size, however the static pressures are different. The following example corresponds to these characteristics.
Thrust by Sails
At B, the air is blown along the front side of the sail. The energy-input is relative small because the convex face of the sail builds a suction area. The static air-pressure is reduced (green arrow), while the total atmospheric air-pressure weights onto the rear side of the sail (red arrow). The difference of pressures result a thrust force. The generated force is stronger than the causing flow because the ´free available energy´ of the normal atmospheric pressure is used (and why a sailboat at side-wind- and diagonal-forward-curse is running faster than the original wind is blowing).
At C, this effect is used double: butterfly-sails are installed symmetric at both sides. The air is blown off the central hollow mast (white and blue) along the front faces of the sails (see arrows). When an airstream is coming up, the air is just ´drawn-off´ the nozzles. An analogue technique is used for reducing the icing-up at the front parts of wings. Few energy-input is demanded for the transport of warm air, because it´s automatically sucked off the conic pipes and nozzles.
The air flow must keep smooth to the front side of the sails in order to minimize the static pressure. Opposite the complete atmospheric pressure weights on the rear side only if there are no turbulences. Most calm air would exist within a closed room.
That´s why, at D, this arrangement is installed within a closed box (black). The air is still blown off the central pipe and nozzles (white and blue) along the convex faces. In addition at E, now the air is drained off through slots into pipes at both sides. A pump (here not drawn) transports the air back to the central pipe.
Right side of the ´sails´ the air is resting and affects normal atmospheric pressure onto these faces (red arrows). Also left side within the box, the air is nearby resting. The relative strong static pressure pushes the flow around the convex faces into the drain-canals. Direct along the faces the air is fast flowing and thus the static pressure is reduced (green arrows). The whole body thus is shifted towards left. Naturally this arrangement can be installed multiple within one box, like sketched at F.
That circuit of air is no optimum solution. Irrespective of, these theoretic considerations clearly approve, thrust can be achieved also within a closed system - as sure as (theoretically like practically) any sail is able to produce thrust forces, stronger than the causing wind is blowing.
Net Result
It´s most advantageous to use the effect of suction. The air follows a back-stepping wall without resistance up to sound-speed. At the bowl-engine in shape of a cone (C) this is achieved, because the cone-mantle represents a continuous suction area into turning sense of the system. The rotor-blades are drawing the air only along these convex face, on and on, with most few resistance and thus demanding minimum energy input.
Also at the sails, the wind-pressure is less important. The compete force of the wind is only used with balloon-riding or if a sailboat is moving into direction of the wind. Multiple faster the boat is pushed through the water by the atmospheric pressure, if the pressure at the front side of the sail is reduced. The necessary air flow can be created also artificially (D), if air is blown along the front side of the sail.
Instead pushing the air through nozzles, again it´s much more effective, the suck-off the air at the rear end of the sail (E), just like at the upper face of a wing, where the suction at the rear end produces most strong flow along the curved nose further ahead. Here, a suction-pump delivers the air back to the outlet-nozzles. At free environment, the airstream would support that air-circulation.
This ´sailing with artificial wind´ however can also be done within a closed system. At the ´sail-boat´ sketched at G, many sail-faces are drawn within the fuselage, where the air-circulation (white) is done by pumps below. Without any doubts thus it´s approved, air movements within a closed box in general can result external affects, here e.g. the thrust for a boat.
Here the air is pulled over a curved right-angle face from one edge to the opposite. However, the air transport within that pipe-system won´t be really flow-conform. Opposite, at the bell-shaped bowl-engine (F), the face is curved into two directions. The air simply is guided around that round-curved face, all times along the convex surface at circled track, so without demanding any back-flow. There is only a synchronous rotation of the rotor and the air. So the cone- and bell-shaped bowl-engines will be much more effective than the previous examples (which nevertheless approve the validity of the general principle).
That ship with it´s fuselage filled up with sails (G) remembers a sailing ship, which - instead of normal sails - had mounted rotating round cylinders (H). These ´Flettner-Cylinders´ were most effective, e.g. a huge cargo-ship with an engine of only %0 HP did cross the Atlantic in 1926. However the times of freight-sail-ships were past, so that invention did fall into oblivion. If now however, that technology could be applied also within a closed system, quite new possibilities would result - like discussed at the following chapter ´Flettner-Box´.
Final Doubts
If air is blown along a vertical wall (B, see arrows), the static pressure (green) is reduced there. At the opposite side is weighting the normal air-pressure (red). If that wall is installed at a vehicle, it will roll towards left (at this example). It does not matter, if a second wall C is installed further left, because normal air-pressure is weighting force-neutral at both sides.
By likely principle, the pressure is reduced at one side at a round face (D, green), if the air is rotating along with a ´whirl-tool´ (blue). In order to protect the whirlwind from external influences, the hollow round cylinder can be closed. It´s advantageous to guide the air along cone- or shell-shaped faces (E and F). Multiple units can be installed within one body. At any case, reduced pressure (green) will weight at one side of the separating walls. At the opposite sides, the (nearby) full air-pressure (red) is affecting and shifting the whole arrangement towards left - still according to previous general valid principle.
At G, both half-spheres are connected with a pipe. The left hemisphere is force-neutral, normal air-pressure weights at both sides (and the pipe can even be open at this area). Within the right hemisphere, a rotor (blue) is turning around, so the air is circulating. The full air-pressure, again is shifting the whole arrangement towards left - still according to previous generally valid rule.
Now it´s the question, how much horse-power is demanded to pull the right hemisphere towards right side, against the thrust of the normal air pressure. The force is depending on the size of effecting faces, the speed of internal flows, the quality of the internal surfaces, the distance between both half-spheres and the density of air inside and outside of a closed box.
So now finally might be obvious, also the pressure-relations within a box produce externally affecting thrust forces. Next chapter will show, the forces are strong enough even to push ships through the oceans - and some more.
Evert / 2016-03-31
The ´Air-Pressure Bowl-Engine´ is described variously at previous chapters. It´s discussed how that new engine can be used for uplift and thrust of aircrafts. All considerations are done strictly logic and all calculations are based on known formula and facts. Nevertheless some doubts exist about the question, if and why these procedures could really work. Real prototypes could be the real approval. However I have no resources and can´t do that. In spite of, also pure theoretic approvals will solve that problem. As this principle is quite new, it´s hard to find real existing examples. Nevertheless I will show by known facts, the power-effects within these closed systems well can result external effects. At first, picture 05.18.01 once more shows the general principle and data of an example.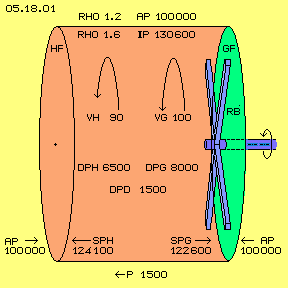 The hollow cylinder is 1 m long and the side faces are 1 m^2, thus the cylinder contains a volume of 1 m^3. The right face is smooth and is called ´glide-face´ GF (green). The mantle of the cylinder is a rough surface and also the left side face, which is called ´stick-face´ HF (red). Rotor-blades RB (blue, simple square profiles) near to the glide-face are rotating with about 2400 rpm, so the air is moving at VG = 100 m/s (as a weighted average) at circles on and on. Further left, the flow is decelerated by friction, so the air near the stick-face rotates slower, e.g. only with VH = 90 m/s.
The hollow cylinder is 1 m long and the side faces are 1 m^2, thus the cylinder contains a volume of 1 m^3. The right face is smooth and is called ´glide-face´ GF (green). The mantle of the cylinder is a rough surface and also the left side face, which is called ´stick-face´ HF (red). Rotor-blades RB (blue, simple square profiles) near to the glide-face are rotating with about 2400 rpm, so the air is moving at VG = 100 m/s (as a weighted average) at circles on and on. Further left, the flow is decelerated by friction, so the air near the stick-face rotates slower, e.g. only with VH = 90 m/s.
Commonly, the thrust for a vehicle is done by support at a medium (e.g. a car at the road, a paddle-steamer at the water) or a medium is pushed backward (e.g. via props within water or air). Also a missile is pushing off gases, working also at the vacuum. At this kind of reaction, the surrounding air is not involved, so this technique should also be possible within a closed system. Picture 05.18.02 left side shows a simple model of well known thrust via reaction.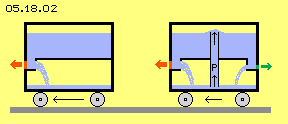 Right side is drawn an additional opening, however showing towards left, with a smaller cross-sectional face. The water pressure weights asymmetric at the face marked green. That pressure is directed towards right side (see green arrow). The water pressure is likely, left and right side. However the green face is smaller, so that force is weaker. Resulting is still a forward directed force, pushing that vehicle towards left side.
Right side is drawn an additional opening, however showing towards left, with a smaller cross-sectional face. The water pressure weights asymmetric at the face marked green. That pressure is directed towards right side (see green arrow). The water pressure is likely, left and right side. However the green face is smaller, so that force is weaker. Resulting is still a forward directed force, pushing that vehicle towards left side.
The bowl-engine is used for thrust and uplift at helicopters. For many readers - at first sight - this remembers the recommendation for a downing man ´pull off yourself by your shock of hair´ or for a yachtsman at lull winds ´you yourself must blow towards the sail´. Less known is the real possibility to result thrust by blowing along the sails, like sketched at picture 05.18.03.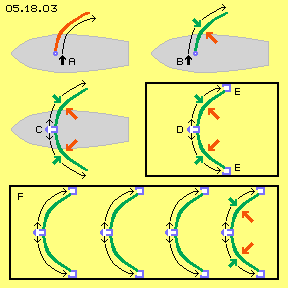 At A the sail (red) is arranged cross to the boat (grey). Also cross to the boat, air is blown along the rear side of the sail. The flow is redirected backward, resulting the thrust force (see arrows). This procedure is not very effective. It would be better to push and move the air direct backward e.g. via prop (even also that technique is not really effective, see chapter ´05.15. Prop- and Jet-Engines´).
At A the sail (red) is arranged cross to the boat (grey). Also cross to the boat, air is blown along the rear side of the sail. The flow is redirected backward, resulting the thrust force (see arrows). This procedure is not very effective. It would be better to push and move the air direct backward e.g. via prop (even also that technique is not really effective, see chapter ´05.15. Prop- and Jet-Engines´).
To sum up these considerations to the pros and cons of the bowl-engines, the results are sketched at picture 05.18.04. At first view is seems impossible, the pressure-relations within a closed system could affect external motions. The simple model of the reaction-effect (A) clearly approves, thrust is affecting at this car, even the water pressures affects pressure of different strength only at the inner side of the walls. However, this (like each) application of pressure is relative ineffective. Here for example, the water must be pumped up for a continuous process.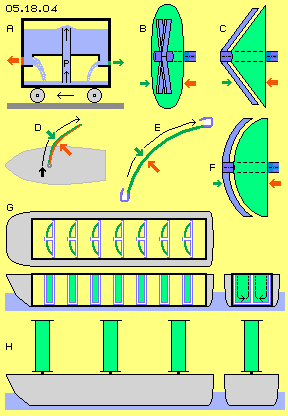 Much more effective is the reduction of pressure. The most simple shape of the bowl-engine (B) just is moving the air at a circle-track along a plane face. Corresponding to the dynamic flow pressure, the static pressure is reduced (green arrow). At the opposite face, the complete atmospheric pressure (of resting air) is weighting (red arrow). It does not demand huge energy input to keep the air rotating, however the normal air-pressure of huge 10 t/m^2 at the opposite face becomes usable.
Much more effective is the reduction of pressure. The most simple shape of the bowl-engine (B) just is moving the air at a circle-track along a plane face. Corresponding to the dynamic flow pressure, the static pressure is reduced (green arrow). At the opposite face, the complete atmospheric pressure (of resting air) is weighting (red arrow). It does not demand huge energy input to keep the air rotating, however the normal air-pressure of huge 10 t/m^2 at the opposite face becomes usable.
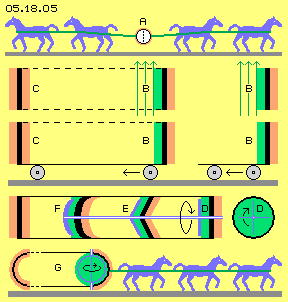 Picture 05.18.05 simplistic shows some facts in order to destroy final doubts. Since ever, man felt the force of winds and feared heavy storms. Finally in 1656 Otto von Guericke demonstrated, also locally resting air is affecting enormous force. At his famous Magdeburger Experiment, he did draw off the air of two hollow half-spheres (A) and even four horses were not able to divide both hemispheres again. Every pupil knows that story. The relation between dynamic flow pressure and static air pressure is much easier to approve, e.g. as every pupil was told to blow over a sheet of paper.
Picture 05.18.05 simplistic shows some facts in order to destroy final doubts. Since ever, man felt the force of winds and feared heavy storms. Finally in 1656 Otto von Guericke demonstrated, also locally resting air is affecting enormous force. At his famous Magdeburger Experiment, he did draw off the air of two hollow half-spheres (A) and even four horses were not able to divide both hemispheres again. Every pupil knows that story. The relation between dynamic flow pressure and static air pressure is much easier to approve, e.g. as every pupil was told to blow over a sheet of paper.
ap0518e.pdf
is the print-version of that chapter.
Flettner-Box
Aero - Technology