Impossible
At this picture at B the ´Magnus-Effect´ is sketched: a water jet not only is redirected below of a curved surface (here towards right) but the round body by itself is dragged into the stream (towards left), even thus far, the water jet at first is redirected towards left. That astonishing strong force is easy to detect by a simple experiment, when holding a spoon below a water tap. The atmospheric pressure is one kilogram each square-centimetre - and the water jet keeps off that strong force from the spoon.
Paradox
That ´lapse´ is explained by the assumption, real fluids are no ´ideal gases´, i.e. lastly are compressible, collisions won´t occur totally elastic, pressures are not transported without loss. That´s valid for solid bodies within water or within air, without any doubt.
However, why can atoms and molecules of gases obviously move without loss? Two answers are possible: 1. because these particles move within pure Nothing - however for me still is paradox, why any Something at its outer borders won´t dissolve immediately into neighbouring Nothing. 2. because ´material particles´ move within a really ideal gas - and null-compression and null-pressure-loss and total-energy-constant only exist within a gapless medium, described in detail at my Aether-Physics and -Philosophy.
Incredible
These abilities are knows since hunters and anglers exist and everybody can know that ´phenomenon´ finally since many decades, as Viktor Schauberger described theses processes in details and developed a ´Trout-Motor´ (which probably didn´t really work). For me it´s phenomenon how cool physics (here especially bionics) take that ´paradox´ appearance instead of making it to the main issue of investigations, with all available resources. So I´ll try, by modest means, to offer some solutions.
Speed, Pressure and Suction
Depending on the speed, a pressure weights on the surface of the cylinder. Front-side at the dam-up-point B exists the dam-up-pressure P1 (red), correlating by square of the basic-speed. Further aside of the cylinder, water flows increasingly faster, so the static pressure decreases towards outside. Most fast speed exists aside of the cylinder, so there comes up a suction-effect (blue), affecting each radial to the centre of the cylinder, e.g. at point F by scale of P-3.
The flows and also the relations of pressures are symmetrical (like drawn here) at ´under-crucial´ speeds. At the rear end (at E) the waters meet and produce a corresponding dam-up-pressure P1, affecting towards left. Theoretical that cylinder would nearby (and a spheres in total) rest within the flow without resistance. As soon however the speed becomes ´over-crucial´, the water at the rear end can´t flow fast enough to the middle and can´t dam up, so the rear-end forward-pressure changes into backward-suction.
Redirection by Power
At picture 05.09.04 such a flow-conform body A (grey) schematic is shown, e.g. the fuselage of an airplane. The body moves within resting air towards left, so the dam-up-pressure B (red) comes up at front side. Aside of exists accelerated flow and thus less static pressure resp. that suction D reaching back to the rear end C. The area of forces showing towards left are marked blue, forces showing towards right (thus against movement) are marked red.
Inevitably however are the backward showing suction-forces C (red), which are marked right side of the picture by their components into longitudinal axis. No matter how long the body is stretched, that ´rear-end-suck´ can not be eliminated in total. So the real resistance of a flow-conform body primary does not occur by dam-up pressure at the bow but by sucking of the tail.
Picture 05.09.04 below shows an early drawing of my Fluid-Technology, a longitudinal cross-sectional view of a ship-body E (grey). The dam-up-pressure at bow F is eliminated as the water (red) is guided aside through canals G via props (dark red). At stern are installed corresponding canals and props, so the rear-end-sucking is also eliminated. This ship is well to maneuver - however that technique is only suitable for ´calm conditions´ e.g. at inland waters.
Mechanic Tension
As an alternative, the below half of that hollow sphere (yellow) could be build by elastic material. From backside F again the normal body-pressure affects onto that ´balloon´, towards frontside-aside G however, this elastic wall would become beat-out towards the outside-suction (like the tarpaulin of lorries). That tension affects a drag at the supporting points, at the mouth cross to the flow and aside at H in forward direction. Is this the effect why trouts stand ´smart´ within flows?
Coanda plus Magnus
The dam-up-pressure B gets into the body through the mouth. The border of mouth C is rounded, so (according to Coanda) the flow D is redirected aside. At the following that cross-flux again is flowing along a curved face E, so the flux F is redirected outward-back. The flux exits through slits into the flow outside of the body resp. is even pulled off by that flow.
So the dam-up-pressure inside of the mouth, no longer affects only as ´resting´ water. That area of ´high density´ however produces a flow, which becomes increased by suction at the outlet of these ´canals´. Flows of different speeds are generated by smart organisation of flow directions and these differences generate the drive forces into the movement direction of the body.
Multiplication of effective Faces
Fishes have grills aside within the head by which they take oxygen dissolved within water (and the water finally exits through grill-slits). Grills generally must show wide surfaces (like lungs) e.g. by tree-like branching. I never looked into the mouth of a living fish, however I am quite certain, special abilities of the brook trout and salmons are based at special shape of their grills (like also Viktor Schauberger assumed).
In principle, these grill-trees and -branches must show relative even and smooth faces at front-sides, while the rear-sides are uneven and rough, e.g. like here sketched by branches or ´hairs´. Along the even surface of front-sides exist fast flows, while at each back-side many turbulences exist with corresponding high static pressures. The pressure differences result ´suction´ into movement direction (here each marked blue). The grills probably are build by fractal structure, so at given space huge surface in total is installed and the pressure differences affect at these multiply surfaces.
Living beings often are build by most elastic materials and thus successful principles of nature sometimes are hard to detect and rarely to copy by total likely techniques. The basic principle of salmons for balancing the resistances against flows and the generation of drive however seems totally clear and simple: multiplication of surfaces opposed to flows and organisation of internal flows that kind, at each front-side face comes up a faster flow than at each rear-side face. That simple principle is easy to rebuild by many designs and techniques.
Principle of technical Solution
At the back-side E are installed sheets in horizontal and vertical direction. The sheets are covered with holes, so the air is hindered to flow fast along that surface. Based on slow movement resp. turbulences, a strong static pressures weight at that surface (thus pushing the airplane forward).
At F is shown a construction which corresponds somehow to previous ´grill-hairs´: the back-side is build like a ´nail-bed´, i.e. many round sticks reach out of surface. The air can move within, however only rather slow and turbulent. Probably elastic elements (like long-hair rough fur or feathers) would work well for producing the wanted high static pressure at the back-sides of the canals.
At G now is sketched a construction of most simple technique, as the back-sides simply show a waved surfaces. The air moving cross over these waves can not flow laminar but only by turbulent vortices. So at any case front-side surfaces of the canals should be most even and smooth, while all back-sides should hinder the flows alongside its surfaces.
Dents and even Surfaces
Further right side, a cross-sectional view is shown and four walls W between the fuselage front-side D and fuselage inner wall A are drawn. Each back-side shows that dent pattern (also right side of the fuselage outer wall) while each front-side is even (also left side of fuselage inner wall). Along the even surfaces, the flows move without resistance, resulting suction (marked blue) respective the difference of static pressures pushes the airplane forward.
Once more further right side, that cross-sectional view is sketched once more, now however the whole ´sandwich´ of sheets is bended corresponding to the curvature of the fuselage bow. Through these canals thus shall move flows with quite different characteristics at both faces. The laminar flow at the front-sides however can not keep at surface very long, but only ten or fifteen times the distance between the surfaces. That´s why here the length of ´sandwich-blocks´ is limited and arranged with some free space between.
Grooves cross- and longwise
At back-sides exist turbulent flows as the cross-grooves won´t allow a continuous flux. Opposite at the front-sides, the flux will run pretty well as the longitudinal grooves protect against disturbances from aside (like known at wings). However also these sandwich-blocks should not be too long and arranged with some distance between, so the wanted flow-pattern can regenerate. In general, laminar flows keep longer at bended surfaces, so curved sandwich-blocks could be some longer (where the bends naturally should always back away from the flow-direction).
Examples of Arrangement
Downside at this drawing is shown, the dam-up-pressure well could enter further inside the fuselage, so the canals resp. sandwich-blocks E are arranged also aside each other. At any case exists high pressure resp. relative high density within that inlet area, from which the air is pressed into the canals. The inlet of the canals are arranged stepwise.
Diverse measurements are possible for increasing the effective faces. Theoretical that technique should also work by micrometers of groove-depth and distances between the walls, practical like ceramics with ordered structures. At the other hand, compressed air becomes relative ´viscous´ and dirt particles will close canals with too less size. So a reasonable scale will be some millimetres or centimetres.
Examples of Data
Now it´s assumed, the flow at the cross-grooved back-sides moves by speed of only 13 m/s, while the flow at longwise grooved front-sides moves by 17 m/s (V 13 resp. V 17). The difference of the kinetic energies of both ´part-flows´ results about 60 N/m^2 (P 60). Correspondingly behave the static pressures at both faces and the difference functions as thrust force.
Six canals (K 6, red lines) are installed here, each wall about 1 cm thick and the distance between the walls some 4 cm. The inlet area of the canals in total thus is about 25 cm (E 0.25) wide and the constructional element in total about 30 cm (B 0.3) wide. The height of the fuselage is assumed 3 m (H 3.0, grey), effective usable height for the sandwich-blocks however is only the half of (H 1.5). A fuselage segment of 1 m widths thus has 6 times 1.5 equal 9 m^2 effective surface (F 9). Onto that total surface now affect previous 60 N/m^2 * 9 m^2 = 540 N as drive-force.
Downside at this drawing, the data of the flight phase are mentioned as an example. The flight speed is assumed with 720 km/h resp. 200 m/s (V 200). However only a part of the dammed-up air shall enter the inlet area, e.g. by 50 m/s (V 50), because the rest of the air must cause the redirection of the flow outside along the bow). Within the canals, the speed again will be reduced, e.g. to 25 m/s (V 25). If again the flows at pressure- and suction-side differ by +/- 2 m/s, the motions will be 23 m/s resp. 27 m/s (V 23 and V 27), the pressure difference now is about 100 N/m^2 (P 100). Related to previous 9 m^2 total surface, the acceleration forces shows 900 N.
Drive for any Demand
At A is sketched a ´canal´ of 1 m length and 1 m^2 cross-sectional face. If the air within is resting, the quite normal atmospheric pressure will weight equal at all side-faces. If air is flowing through that canal (here from below up), upside will come up increased dynamic pressure and at the side-faces corresponding less static pressure. Stronger flows will increase the dynamic pressure once more and the static pressure will decrease even more (see arrows at A and B). If that wide canal is divided into ten narrow canals, the static pressure will weight at ten times wider faces of the walls between.
At this table the dyamic pressure again is calculated by common formula P=0.5 * m*rho*v^2, for each speeds at pressure- and suction-sides (VD and VS). The pressure-difference between pressure- and suction-side (PD und PS) is the thrust-pressure (PV). Both two upside rows show previous 60 N/m^2 und 100 N/m^2.
As these canals are rather wide (with the distance of 10 cm between the walls), also higher throughput could be achieved. Same time, the difference of speed at both sides could be wider, e.g. at the start already with 18 and 23 m/s (see third row), resulting a thrust of 102 N/m^2. At high-speed travel (see forth row), the air could move e.g. by 30 and 36 m/s, resulting the thrust-force of 198 N/m^2.
The available total thurst depends on the total available face. For example, the cross-section of the A380-fuselage is about 80 m^2. Some 50 m^2 could be used for the Trout-Thrust-Engine. At the middle right side of picture 09.05.13, schematic is shown a cross-section (D) and a longitudinal cross-sectional view (E). The cockpit (light grey) could be arranged at the center. The inlet for the dam-up-pressure is ring-shaped and marked red. As a thrust-face (blue) is available a ring of about 50 m^2. The outlet of the canals is done via ´gill-slots´ al around the fuselage (dark grey).
At a length of e.g. 3 m could be installed 25 canals. So an effecting face of 50 * 25 = 1250 m^2 will be available (much more than the surface of the wings). Assuming a pressure of about 100 N/m^2, the thrust in total would be 125 kN - or at a pressure of 200 N/m^2 would result the double thrust with 250 kN. At high flight-level with less air-density, the real usable thrust would be some 100 kN. That´s enough for flying over the Atlantic completely autonomous. The jet-engines are only necessary for the acceleration of the start-phase. The start-weight of the plane is much less, because only the half of commonly demanded fuel must be tanked. And by the way, that airplane will fly without much noise.
One Tenth for Drive
A wing is sketched below right side. At the below face of the wing, the air wanders along with previous 50 m/s = 180 km/h. The curved upper face of the wing generates an additional, ´artificial´ wind of about 50 km/h. So the air sweeps across the upper face with some 230 km/h. By that rough considerations, a relation on 18 to 23 km/h within the drive-canals would be necessary (marked green at that table). These roundabout 100 N/m^2 would be sufficient thrust, if applied at sufficient large faces, at least corresponding to the size of the wings.
Sailing towards the Wind
At B the ´real wind´ is blowing from aside. In addition with the airstream of the ship-speed, the ´seeming wind´ comes from some diagonal-forward. That faster flow results stronger forces at the sail. Only a part of that force is forward directed, nevertheless pushing that ship faster ahead.
Also the upper face of a wing (at D) works like a sail. However here the airstream comes direct from ahead. The lift (directed some upward-forward) exclusively is generated by the accelerated air flow above the wing. Motor power is only demanded for producing the airstream.
Also the upper face of a wing (at D) works like a sail. However here the airstream comes direct from ahead. The lift (directed some upward-forward) exclusively is generated by the accelerated air flow above the wing. Motor power is only demanded for producing the airstream.
This picture right side at E shows a cross-sectional view through the flow-conform body of an airplane fuselage. When that body is moving through ´resting´ air, a dam-up-pressure comes up in front of the bow. Finally however all air flows off alongside the fuselage (marked by arrows).
It won´t produce more resistance, if the dam-up-pressure is allowed to enter into the fuselage and the air may flow off aside some later (like sketched at F).
If now some ´sails´ are installed within the canals, their ´lift-force´ will show straight ahead, driving the fuselage forward (like sketched at G). These ´sail-walls´ must be build by suitable material and in suitable shape with most large surface. So that fuselage will ´sail´ just into the wind direction and produce the demanded airstream autonomously by itself (at least by major part).
Some students and members of the institutes for air- and space-sciences at the university of Stuttgart already achieve a similar solution: they installed a prop respective a ´wind-mill´ at a simple car, generating autonomous drive from its own airstream. Only for starting the system, some manual push was necessary, afterward that car did move forward continuously (lat. ´perpetuum mobile´). That´s not possible or at least not welcome by common understanding (and probably that´s why that most successful experiment is merely to find within open literature).
However that process does not injure the law of energy constant: the energy of molecular motions is only temporary organizes that kind, a usable side-effect comes up. Just that´s the idea of that Trout-Thrust-Engine, in direct manner, without any rotation elements, but based only at the shape of walls and the organization of suitable flows.
Subject of this chapter is the resistance-free drive of bodies within fluids, so e.g. an airplane will go on flying without motor drive. By all rules of physics that seems impossible - however neither a bumblebee nor a brook trout did study natural sciences. And many other physical appearances appear impossible at first sight. At picture 05.09.01 at A for example the ´Coanda-Effect´ is sketched: water (blue) flows off a pipe and meets a rounded face (grey) aside and is redirected along that surface - out of the original direction of its inertia like gravity. Physicians easy can explain that ´impossibility´ by theoretic formula (e.g. concerning ´circulation´), while I explained the real processes and effects based on normal molecular movements at previous chapters. One of my provocative statements now is confirmed: flows have no compelling inertia but particles all times move that direction where the distance to next collisions are most long - even right angle to previous direction of the flow.
At picture 05.09.01 at A for example the ´Coanda-Effect´ is sketched: water (blue) flows off a pipe and meets a rounded face (grey) aside and is redirected along that surface - out of the original direction of its inertia like gravity. Physicians easy can explain that ´impossibility´ by theoretic formula (e.g. concerning ´circulation´), while I explained the real processes and effects based on normal molecular movements at previous chapters. One of my provocative statements now is confirmed: flows have no compelling inertia but particles all times move that direction where the distance to next collisions are most long - even right angle to previous direction of the flow.
At this picture at C schematic is sketched the Paradox-d´Alembert: a body moves through fluid and affects pressure towards front side. As all pressures immediately spread into all directions likely, the pressure lastly affects also at the rear side of the body, by same strength (as a continuous process if the body moves steady through the fluid). Thus that motion should be without resistance and the body would go on moving without losses. This is valid not only for spheres but also for any flow-conform body, like e.g. sketched at D. No matter that profile moves towards left or right side, the forces are symmetric - however ´paradoxicial´ also these bodies show resistance. Here however the subject are movements within the world of particles, e.g. of a flow-conform body (E at previous picture) moving through the m medium of air. Based on all experiences, resistance will comes up. Only by the input of energy that body goes on moving.
Here however the subject are movements within the world of particles, e.g. of a flow-conform body (E at previous picture) moving through the m medium of air. Based on all experiences, resistance will comes up. Only by the input of energy that body goes on moving.
Paradoxicial however some ´bodies´ are able to move relative to fluid obviously without resistance. Maybe someone was astonished when detecting fishes high up at mountain streams. The brook trout stand totally motionless within a flow and at dangerous situations flee like a flash - upwards against the flow. These fishes are born up there, however some of these species (e.g. salmons) wander down to the ocean - and back again, even through meter-high waterfalls.
Picture 05.09.03 shows a drawing of textbook for description of previous Paradoxon-d´Alembert. A round cylinder (grey) is positioned within a flow. Far ahead of the cylinder, left side at A, the flow shows speed V1 (marked by vertical line). Towards front-side point B of the cylinder, the flow is dammed up so theoretic exists no motion (V0) at that ´dam-up-point´.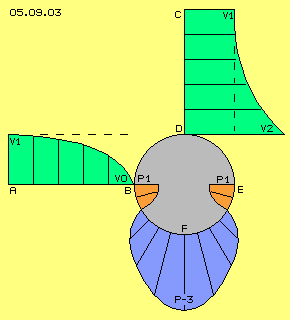 Aside of the cylinder, also are marked speeds, far outside at C again that basic-speed V1 (horizontal line). Towards the cylinder the speed becomes faster and direct at the surface D it shows ´over-speed´ V2, nearby double of the basic-speed.
Aside of the cylinder, also are marked speeds, far outside at C again that basic-speed V1 (horizontal line). Towards the cylinder the speed becomes faster and direct at the surface D it shows ´over-speed´ V2, nearby double of the basic-speed.
Thus in general, the resistance of round bodies is balanced, showing likely pressure and suction. However, a negative suction exists at the rear end. The flanks of a body must be long stretched in a ´flow-conform shape´ to reduce that ´rear-end-suck´.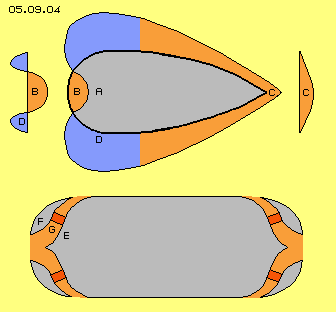 Suction forces affect right angle towards the face, i.e. the forward and back showing components mostly are only a parts of. These force-components of the bow-area are marked quite left side of the picture, dam-up-pressure B red and suction-components D blue. These longitudinal forces at the bow of the body are balance.
Suction forces affect right angle towards the face, i.e. the forward and back showing components mostly are only a parts of. These force-components of the bow-area are marked quite left side of the picture, dam-up-pressure B red and suction-components D blue. These longitudinal forces at the bow of the body are balance.
The real solution of that problem might be solved by brook trouts. Obviously they can reduce the flow resistance to zero and above this, they produce a drive force relative to flow - without motor power. At picture 05.09.05 the body A of a trout is drawn schematic as flow-conform profile. The trout stands still within the flow with open mouth, so the dam-up-pressure B (red) also affects inside of the body. The areas of suction D aside, reaching up to rear end C, again are marked blue.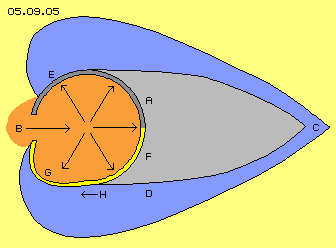 Arrows within the mouth-area represent the dam-up-pressure, affecting all around likely. That increased pressure thus affects also onto the upper wall (dark grey), which could be the inner side of a half sphere. From the rear side, i.e. from the body A, affects normal counter-pressure at this sphere. Opposite, at front side of that sphere affects much less pressure from the suction-bow-area. So that inner sphere would be pressed forward - a very smart solution of the paradoxon. ´Much too smart?´.
Arrows within the mouth-area represent the dam-up-pressure, affecting all around likely. That increased pressure thus affects also onto the upper wall (dark grey), which could be the inner side of a half sphere. From the rear side, i.e. from the body A, affects normal counter-pressure at this sphere. Opposite, at front side of that sphere affects much less pressure from the suction-bow-area. So that inner sphere would be pressed forward - a very smart solution of the paradoxon. ´Much too smart?´.
The dam-up-pressure is a positive occurrence as forces come up. Previous solutions however use these forces only static, so not according to the special behaviour of fluids. Remarkable and most effective forces only come up by flows, like e.g. by previous mentioned Coanda- and Magnus-Effect. Picture 05.09.06 shows only the front part of a body A. The areas of dam-up-pressure (respective slow flows) are marked red and the areas of suction (resp. faster flows) are marked blue. At first is discussed the drawing left side of the picture. Simultaneously with the redirections of flows, each surface is pressed to the flow (according to Magnus). At mouth C thus affect forces G into centripetal directions, thus neutral. At the second bending however, the surface H is pulled forward. So by that double redirection, the static dam-up-pressure is transferred into dynamic a drive-force. Behind the round mouth come up turbulences J, which inside affect stronger pressure onto the ´cheek´ (I), while outside exists only small static pressure at that suction area.
Simultaneously with the redirections of flows, each surface is pressed to the flow (according to Magnus). At mouth C thus affect forces G into centripetal directions, thus neutral. At the second bending however, the surface H is pulled forward. So by that double redirection, the static dam-up-pressure is transferred into dynamic a drive-force. Behind the round mouth come up turbulences J, which inside affect stronger pressure onto the ´cheek´ (I), while outside exists only small static pressure at that suction area.
At this picture right side now the basic construction of that ´Salmon-Drive-Engine´ is sketched. Again only the front part of body A is drawn and the elements are marked correspondingly. Additional ´constructional element´ of grills K schematic are drawn.
Picture 05.09.07 shows the fuselage of an airplane (moving towards left within resting air) with an example of the basic principle for a technical solution. Here the fuselage shows a broad nose (like used at the following chapter). In front of the fuselage A exists the dam-up-pressure B which enters the space inside of the body. A flow within canal C (between fuselage A and part D of the body) is redirected at curved faces and exits aside through slits. So at the one hand, the air is pressed into canals by the dam-up-pressure, at the other hand the air is sucked off the canals by flows along the outer surface of the body.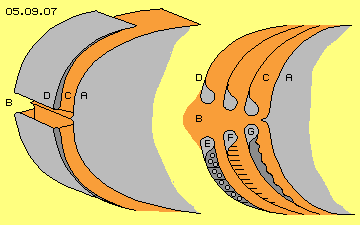 At this picture right-upside once more is shown the redirection at bended faces within three canals C, each showing two walls. Here, the ´back-side´ is called each surface showing to the tail of plane. The ´front-side´ is called each surface showing towards the bow of the plane. At this picture right side below schematic are drawn three possibilities for decelerating the flow at back-sides.
At this picture right-upside once more is shown the redirection at bended faces within three canals C, each showing two walls. Here, the ´back-side´ is called each surface showing to the tail of plane. The ´front-side´ is called each surface showing towards the bow of the plane. At this picture right side below schematic are drawn three possibilities for decelerating the flow at back-sides.
Previous pictures are pure schematic drawings and much too ´macroscopic´. Certainly, fluid needs enough space to move, e.g. sufficient diameters of pipes and here of the canals. Otherwise the system will stop the throughput by itself. On the other hand these grills show, the effect comes up only by an enormously increased surface, i.e. at microscopic small structures. As here the flow is pushed by pressure and same time it´s dragged off the canals, also relative narrow canals should work.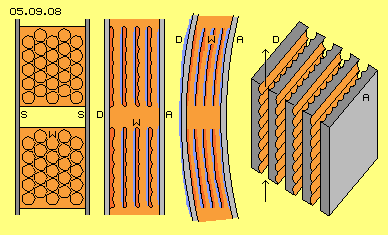 At picture 05.09.08 previous ´back-side with waves´ is shown some more detailed, as the waves here are replaced by small dents. Left side of the picture shows a view onto the back-side W, which is mounted between two beams S. The circles represent small round dents, or also a honeycomb pattern would work likely. The air moves along these holes by much turbulent flow.
At picture 05.09.08 previous ´back-side with waves´ is shown some more detailed, as the waves here are replaced by small dents. Left side of the picture shows a view onto the back-side W, which is mounted between two beams S. The circles represent small round dents, or also a honeycomb pattern would work likely. The air moves along these holes by much turbulent flow.
At picture 05.09.08 quite right side is sketched a sandwich-block by diagonal view, which might be easy to construct and might be most effective too. The air flows downside up through canals, each back-side shows grooves cross to flow, each front-side shows grooves into direction of the flow. So each wall has grooves at both side, at one side longitudinal and at the other side cross to the flow.
At picture 05.09.09 left side, again the bow of fuselage A is drawn inclusive the front part D of the body and canals C between. At the bow exists a dam-up-pressure, so the air is pressed into the canals (and also pulled off aside). Upside at this drawing, previous sandwich-blocks (dark red, with each distances between) are arranged corresponding to the curvature of the bow.
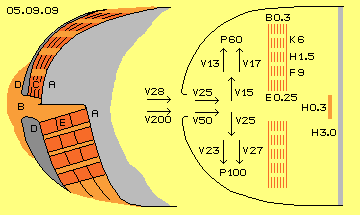 At picture 05.09.09 right side are mentioned some data as an examples, upside of the start-phase and below the flight-phase. When starting, the airplane e.g. moves only by 100 km/h, thus by about 28 m/s (V 28) relative to the resting air, respective the air comes to the inlet with this speed. At that area, the air becomes dammed up and the speed is reduced e.g. to 25 m/s (V 25). Into the relative narrow, upward showing canal the air will flow again some slower, e.g. only by 15 m/s (V 15).
At picture 05.09.09 right side are mentioned some data as an examples, upside of the start-phase and below the flight-phase. When starting, the airplane e.g. moves only by 100 km/h, thus by about 28 m/s (V 28) relative to the resting air, respective the air comes to the inlet with this speed. At that area, the air becomes dammed up and the speed is reduced e.g. to 25 m/s (V 25). Into the relative narrow, upward showing canal the air will flow again some slower, e.g. only by 15 m/s (V 15).
Drive for any Demand
That thrust of 900 N naturally is rather small, e.g. in comparison with the 300 kN for starting the A380 plane. At previous chapter were discussed the lift-forces at wings by speeds and pressures within one cubic meter of air. Analogue data are shown at picture 05.09.13, now concerning that trout-thrust.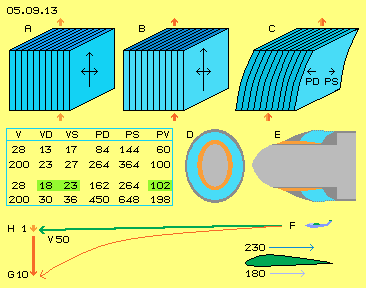 Now it´s important, the canals are curved, e.g. like drawn at C. Already this will result a difference of flow-speeds: the flow will hit onto the concave (pressure-) face, friction will come up and a reduced flow. Along the convex (suction-) face, the air continuously can fall into relative void, resulting an ordered and accelerated flow. In addition, naturally the faces should be rough at the back-side and most even at the front-side. Resulting will increased static pressure at the (pressure-) back-sides and reduced static pressure at the (suction-) front-sides (see arrows PD and PS at C).
Now it´s important, the canals are curved, e.g. like drawn at C. Already this will result a difference of flow-speeds: the flow will hit onto the concave (pressure-) face, friction will come up and a reduced flow. Along the convex (suction-) face, the air continuously can fall into relative void, resulting an ordered and accelerated flow. In addition, naturally the faces should be rough at the back-side and most even at the front-side. Resulting will increased static pressure at the (pressure-) back-sides and reduced static pressure at the (suction-) front-sides (see arrows PD and PS at C).
Below at picture 05.09.13 is sketched a glider F, flying towards left by 50 m/s. Without the lift-force of its wings, it would fall down with the gravity acceleration of about 10 m/s^2 (red curve from F to G). That glider is build most streamlined, nevertheless it´s decelerated by air-resistance, becomes slowed down, loosing corresponding of lift-force. In order to balance the resistance, the glider must fall down at an ´inclined plain´ (see line F to H), e.g. 1 m height at a distance of 50 m. So one tenth of the gravity, here 1 m/s^2, are necessary for keeping the speed constant.
Left side at picture 05.09.14 are drawn some sailing ships, showing some well known facts. At A the wind (black arrow) is blowing from astern, the sail stands cross to the wind, driving the ship forward (red arrow), against the water-resistance, some slower than the wind is blowing. If the wind blows even more from forward direction (at C), in addition with the ships airstream, much heavier forces come up, e.g. tilting the ship aside. Nevertheless that ship will run much faster through the waves than the
energy of the original wind by itself could achieve.
If the wind blows even more from forward direction (at C), in addition with the ships airstream, much heavier forces come up, e.g. tilting the ship aside. Nevertheless that ship will run much faster through the waves than the
energy of the original wind by itself could achieve. Naturally this sounds incredible - however that´s just what each trout does: standing still within a flow and if it looks dangerous tit flees like a flash, up into the flow direction. They also do some turns within a basin below a water fall until jumping up for meters. Only these beings obviously are able tor transfer the dam-up-pressure into drive-forces. Specialists of flow-techniques and especially of the air- and space-sciences should take up that challenge and they will be able to realize these techniques.
Naturally this sounds incredible - however that´s just what each trout does: standing still within a flow and if it looks dangerous tit flees like a flash, up into the flow direction. They also do some turns within a basin below a water fall until jumping up for meters. Only these beings obviously are able tor transfer the dam-up-pressure into drive-forces. Specialists of flow-techniques and especially of the air- and space-sciences should take up that challenge and they will be able to realize these techniques.
05.08. Airplane NT
Aero - Technology